1ª ACQF
| QUESTÃO: 1 | ||
Encontre a transformada de Laplace de F(t)=t².
|
||
| F(s)=2/s4 | ||

|
F(s)=2/s3 | |

|
F(s)=1/s3 | |
| F(s)=2/s | ||
| F(s)=2/s2 | ||
1ª ACQF
QUESTÃO 01
Um sistema físico tem como entrada a variável u(t), e como saída a variável y(t).
A equação diferencial utilizada para representar o comportamento dinâmico do sistema é:
4.d2y(t)/dt2+2.dy(t)/dt+y(t)=r(t)
A função de transferência do sistema, portanto, será:
A equação diferencial utilizada para representar o comportamento dinâmico do sistema é:
4.d2y(t)/dt2+2.dy(t)/dt+y(t)=r(t)
A função de transferência do sistema, portanto, será:
| 2/(s2+2.s+1) | |
| 1/(2.s2+4.s+1) | |
| 1/(4.s2+2.s+1) | |
| 4/(s2+s+1) | |
| 4/(4.s2+2.s+1) |
2ª ACQF
QUESTÃO 01
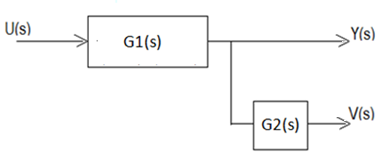
Um sistema de controle de posição de braço de robô tem como variável de entrada tensão u(t), dada em volts, e pode ter duas variáveis de saída: velocidade v(t) dada em metros por segundo, e deslocamento y(t) dado em metros.
O comportamento dinâmico do sistema é dado pela equação diferencial:
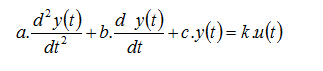
sendo k=1, a=1, b=3 e c=2.
As funções de transferência G1(s) e G2(s) que permitem representar o sistema pelo diagrama de blocos abaixo, são:
O comportamento dinâmico do sistema é dado pela equação diferencial:
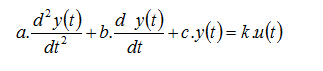
sendo k=1, a=1, b=3 e c=2.
As funções de transferência G1(s) e G2(s) que permitem representar o sistema pelo diagrama de blocos abaixo, são:

2ª ACQF
QUESTÃO 03
A figura abaixo apresenta o diagrama de controle de um processo de aquecimento de água em um trocador de calor, usando vapor superaquecido como fonte de energia térmica.
Nos quadros numerados cabem os termos técnicos, processo, controle, sensor, controlador e atuador.
.png)
2ª ACQF
| QUESTÃO: 1 | ||
Dada a função de
transferência F(s)=1/(2.s+2), encontre o seu valor final para um degrau
unitário de valor 1, e assinale a alternativa correta.
|
||
| 2 | ||
| 1.5 | ||
| 2.5 | ||

|
0.5 | |
| 1 | ||
| QUESTÃO: 2 | ||
Dada a função de
transferência abaixo encontre o seu valor final para um degrau unitário
de valor 2, e assinale a alternativa correta.
F(s)=1/(2.s+2) |
||
| 5 | ||
| 4 | ||

|
1 | |
| 2 | ||
| 3 | ||
| QUESTÃO: 3 | ||
Dada a função de
transferência F(s)=1/(s+2)^2, encontre o seu valor final para um
degrau unitário de valor 1, e assinale a alternativa correta.
|
||
| 0.50 | ||
| 1.00 | ||
| 1.25 | ||
| 0.75 | ||

|
0.25 | |
| QUESTÃO: 1 | ||
Dada a função
F(s)=1/(s²+2) , encontre o valor final para um degrau unitário de
amplitude 2.
|
||
| 5 | ||

|
1 | |
| 3 | ||
| 4 | ||
| 2 | ||
|
|
| QUESTÃO: 1 - TEMPO UTILIZADO: 00:00:52 | ||
A figura abaixo mostra um servo-sistema posicionador de braço de robô, onde K é o ganho ajustável de um controlador, utilizado para realizar o controle posição do braço.
.png) Ao lado da figura estão relacionadas 5 opções para cálculo de fator de amortecimento e frequência natural, em função do ganho do controlador K, enumeradas de I a V. Qual delas é a correta? | ||
| III | ||
 | IV | |
| I | ||
| II | ||
| V | ||
| QUESTÃO: 2 - TEMPO UTILIZADO: 00:00:35 | ||
O diagrama de blocos da figura abaixo apresenta um sistema de controle em malha fechada de primeira ordem. K é o ganho do controlador, Kp e Tp são o ganho e a constante de tempo do processo.
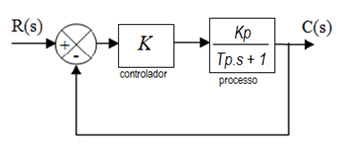 Determine as expressões para cálculo do ganho (Gmf) e da constante de tempo (τmf) de malha fechada, em função deK , Kp e Tp. Considerando a resposta ao degrau do sistema de malha fechada, avalie as sentenças abaixo, e marque a incorreta. | ||
 | A redução do valor do ganho K do controlador reduz a constante de tempo do sistema, tornando suas respostas mais rápidas. | |
| Os parâmetros Gmf e Tmf dependerão do ganho K do controlador. | ||
| Tanto o processo quanto o sistema de malha fechada são de primeira ordem, para quaisquer valores de ganho K do controlador. | ||
| O aumento do ganho K do controlador reduz o erro de regime do sistema, porém não consegue eliminá-lo. | ||
| O sistema sempre apresentará erro de regime, pois o ganho de malha fechada sempre será menor que 1. | ||
4ª ACQF
| QUESTÃO: 1 | ||
Determine a Transformada de Laplace de F(t)=1+t².
|
||
| F(s)=(s+2)/s³ | ||
| F(s)=2/s³ | ||
| F(s)=(s²+1)/s² | ||

|
F(s)=(s²+2)/s³ | |

|
F(s)=(s²+1)/s³ | |
| QUESTÃO: 2 | ||
Encontre a transformada de Laplace da função no tempo abaixo representada pelo gráfico.
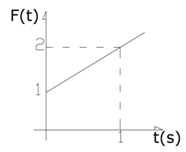 |
||
| F(s)=(1+s)/s | ||
| F(s)=(2+s)/s² | ||
| F(s)=2/s² | ||
| F(s)=(1+s²)/s² | ||

|
F(s)=(1+s)/s² | |
| QUESTÃO: 3 | ||
Determine a Transformada de Laplace de F(t)=1+e-2.t .
|
||
| F(s)=2/s*(s+2)/(s+2) | ||
| F(s)=2/s*(s+1)/(s+1) | ||
| F(s)=1/s*(s+1)/(s+2) | ||
| F(s)=1/s*(s+1)/(s+1) | ||

|
F(s)=2/s*(s+1)/(s+2) | |
|
| QUESTÃO: 1 - TEMPO UTILIZADO: 00:12:38 | ||
O amplificador operacional é um dispositivo utilizado em várias aplicações em circuitos eletrônicos de instrumentação e controle. Sua versatilidade deriva das características de altíssimo ganho, impedância de entrada elevada e impedância de saída baixa.
Para modelar sistemas com AO, assume-se que não entra corrente nos terminais (+) e (-) (impedância de entrada infinita), e que não diferença de potencial entre os mesmos (estão em "curto-circuito virtual"). No sistema abaixo, empregando-se essas considerações, chega-se ao conjunto de equações dado: 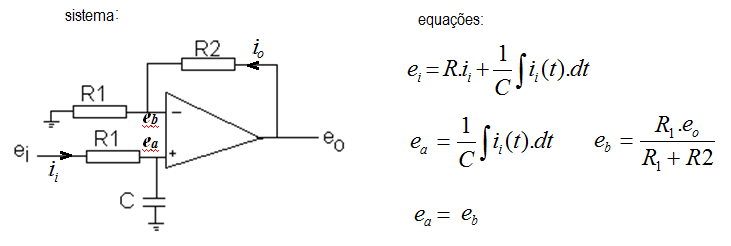 Considerando que a função de transferência do sistema Eo(s)/Ei(s), analise as alternativas abaixo e marque a incorreta. | ||
| A tensão de saída eo(t) em regime permanente sempre será maior que a tensão de entrada ei(t), e ambas terão o mesmo sinal. | ||
| O sistema terá um pólo em s =-1/(R1.C) | ||
| O sistema é de primeira ordem. | ||
 | O sistema terá um zero em s=0 | |
| A função de transferência será do tipo K/(T.s+1), onde K= (R1+R2)/R1 e T= R1.C | ||
| QUESTÃO: 2 - TEMPO UTILIZADO: 05:44:19 | ||
Um sistema de primeira ordem, com função de transferência F(s), recebe excitação de entrada do tipo degrau de amplitude 10, e apresenta resposta c(t) dada no gráfico abaixo.
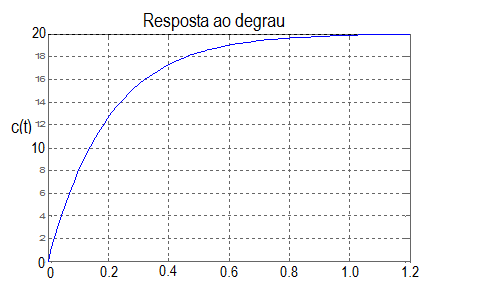 Dentre as opções apresentadas abaixo, qual melhor representa a função de transferência F(s) e a resposta ao degrau c(t)? (considere exp - exponencial de base e) | ||
| F(s)=2/(0,2 s + 1); c(t)=20.(1-exp(-0,2.t)) | ||
| F(s)=10/(0,2 s + 1); c(t)=20.(1-exp(-0,2.t)) | ||
| F(s)=20/(2 s + 1); c(t)=20.(1-exp(-5.t)) | ||
| F(s)=2/(s + 1); c(t)=20.(1-exp(-t)) | ||
 | F(s)=2/(0,2 s + 1); c(t)=20.(1-exp(-5.t)) | |
| QUESTÃO: 3 - TEMPO UTILIZADO: 00:13:13 | ||
Um circuito série, formado pela ligação de um resistor e um indutor é um sistema de primeira ordem.
Considerando vi(t) a tensão da fonte, i(t) a corrente no circuito, vR(t) a tensão no resistor e VL(t) a tensão no indutor, as funções de transferência VR(s)/Vi(s) e I(s)/ Vi(s) serão dadas por: | ||
 | 1/(L/R.s +1) e 1/(Ls+R) | |
| R/(Ls+R) e L.s/(L/R.s +1) | ||
| 1/(Ls+R) e 1/(L/R.s+1) | ||
| L.s/(Ls+R) e R/(L/R.s+1) | ||
| L/(Ls+R) e R/(L/R.s+1) | ||
4ª ACQF
| QUESTÃO: 1 - TEMPO UTILIZADO: 00:12:38 | ||
O amplificador operacional é um dispositivo utilizado em várias aplicações em circuitos eletrônicos de instrumentação e controle. Sua versatilidade deriva das características de altíssimo ganho, impedância de entrada elevada e impedância de saída baixa.
Para modelar sistemas com AO, assume-se que não entra corrente nos terminais (+) e (-) (impedância de entrada infinita), e que não diferença de potencial entre os mesmos (estão em "curto-circuito virtual"). No sistema abaixo, empregando-se essas considerações, chega-se ao conjunto de equações dado:  Considerando que a função de transferência do sistema Eo(s)/Ei(s), analise as alternativas abaixo e marque a incorreta. |
||
| A tensão de saída eo(t) em regime permanente sempre será maior que a tensão de entrada ei(t), e ambas terão o mesmo sinal. | ||
| O sistema terá um pólo em s =-1/(R1.C) | ||
| O sistema é de primeira ordem. | ||

|
O sistema terá um zero em s=0 | |
| A função de transferência será do tipo K/(T.s+1), onde K= (R1+R2)/R1 e T= R1.C | ||
| QUESTÃO: 2 - TEMPO UTILIZADO: 05:44:19 | ||
Um sistema de primeira ordem, com função de transferência F(s), recebe excitação de entrada do tipo degrau de amplitude 10, e apresenta resposta c(t) dada no gráfico abaixo.
 Dentre as opções apresentadas abaixo, qual melhor representa a função de transferência F(s) e a resposta ao degrau c(t)? (considere exp - exponencial de base e) |
||
| F(s)=2/(0,2 s + 1); c(t)=20.(1-exp(-0,2.t)) | ||
| F(s)=10/(0,2 s + 1); c(t)=20.(1-exp(-0,2.t)) | ||
| F(s)=20/(2 s + 1); c(t)=20.(1-exp(-5.t)) | ||
| F(s)=2/(s + 1); c(t)=20.(1-exp(-t)) | ||

|
F(s)=2/(0,2 s + 1); c(t)=20.(1-exp(-5.t)) | |
| QUESTÃO: 3 - TEMPO UTILIZADO: 00:13:13 | ||
Um circuito série, formado pela ligação de um resistor e um indutor é um sistema de primeira ordem.
Considerando vi(t) a tensão da fonte, i(t) a corrente no circuito, vR(t) a tensão no resistor e VL(t) a tensão no indutor, as funções de transferência VR(s)/Vi(s) e I(s)/ Vi(s) serão dadas por: |
||

|
1/(L/R.s +1) e 1/(Ls+R) | |
| R/(Ls+R) e L.s/(L/R.s +1) | ||
| 1/(Ls+R) e 1/(L/R.s+1) | ||
| L.s/(Ls+R) e R/(L/R.s+1) | ||
| L/(Ls+R) e R/(L/R.s+1) | ||
4ª ACQF
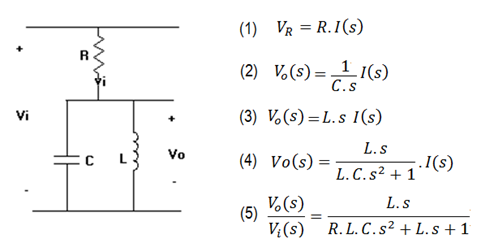
| QUESTÃO: 1 - TEMPO UTILIZADO: 00:27:48 | ||
O sistema elétrico apresentado na figura abaixo é utilizado como filtro em sistemas de recepção de sinais.
Vi e Vo e os sinais de tensões na entrada e na saída do filtro, i é a corrente elétrica. R, L e C são, respectivamente elementos resistência, indutância e capacitância.  Analise as afirmativas abaixo, relativas às informações apresentadas na figura, marque com V as verdadeiras, e com F as falsas. |
||
| ( V ) | A equação (5) é verdadeira e representa a função de transferência do sistema. | |
| ( F ) | O filtro é um sistema de 3a. ordem, e portanto possui três pólos e um zero. | |
| ( V ) | A equação (4) é verdadeira. | |
| ( F ) | Apenas a equação (3) é falsa. | |
| ( V ) | Todas as equações apresentadas são verdadeiras. | |
| ( F ) | Apenas a equação (2) é falsa. | |
| ( V ) | O ganho do sistema filtro é zero. | |
| ( V ) | A equação (1) é verdadeira, porém a (2) e (3) são falsas. | |
| QUESTÃO: 2 - TEMPO UTILIZADO: 00:27:28 | ||
Nas equações apresentas abaixo, c(t) representa possíveis respostas de sistemas de segunda ordem, sujeitos a entrada do tipo degrau unitário.
 As equações (1), (2) e (3) correspondem, respectivamente, a respostas de sistemas: |
||
| Sobreamortecido, subamortecido e criticamente amortecido. | ||

|
Criticamente amortecido, sobreamortecido e subamortecido. | |
| Criticamente amortecido, subamortecido e sobreamortecido. | ||

|
Sobreamortecido e criticamente amortecido, subamortecido. | |
| Subamortecido, sobreamortecido e criticamente amortecido. | ||
| QUESTÃO: 3 - TEMPO UTILIZADO: 00:06:50 | ||
A figura apresenta o esquema elétrico de um sistema com amplificadores operacionais que contém modelos de primeira e de segunda ordem, e sua representação por diagramas de blocos e funções de transferência.
 Analise as informações contidas na figura, e identifique nas sentenças abaixo as verdadeiras e as falsas, marcando-as com V ou F, respectivamente. |
||

|
V | Eo2(s)/Ei(s) é uma função de transferência de primeira ordem, com ganho igual a 3 e pólo igual a -1/(RC). |

|
F | G3 é um bloco subtrator com ganho 2 |

|
V | Eo(s)/Ei(s) função de transferência de segunda ordem, com ganho igual a 1, e pólos iguais a -1/(2RC) e -1/(RC) |

|
F | G1 = 2/(2.R.C.s+1) |

|
F | G2 = -3/(RC.s+1) |

|
F | se ei(t)=1 V, em regime permanente, eo(t)=-1V |

|
V | Eo(s)=( G1+G2).G3.Ei(s) |

|
V | Eo1(s)/Ei(s) é uma função de transferência de primeira ordem, com ganho igual a -2 e pólo igual a -1/(2RC). |
A
habilidade de utilização de modelos para a representação de sistemas é
de extrema importância para o exercício profissional da engenharia. O Engenheiro
deve ser capaz de representar sistemas físicos por modelos matemáticos,
diagramáticos, icônicos, esquemáticos, dentre outros.
A
Figura abaixo apresente o modelo esquemático para um sistema elétrico, e
o modelo diagramático correspondente. Analise as informações contidas
nos dois modelos.
 Considere as equações I, II, III e IV, que relacionam as grandezas elétricas do sistema, no domínio de Laplace: I - Vin(s) - Vc(s) = L1.s.I1(s) II - Vc(s) = (I1(s) + I2(s))/(c.s) III - Vout(s) = R.I2(s) IV - Vin(s) = L1.s.I1(s) - L2.s.I2(s) - R.I2(s) Dentre as alternativas seguintes, identifique a única correta. |
||
| As equações III e IV estão corretas, e representam a tensão de saída e tensão de entrada do sistema, respectivamente. | ||
| A equação II está correta e permite encontrar a tensão no capacitor, representada no diagrama de blocos pela seta 3. | ||

|
A equação I está correta e permite encontrar a tensão no indutor L1 representada no diagrama de blocos pela seta 1. | |
| As setas do diagrama de blocos que representam as correntes I1 e I2 são a 4 e a 2, respectivamente. | ||
| A tensão no indutor L2 está representada no diagrama de blocos pela seta 5, e pode ser calculada pela equação III. | ||
| QUESTÃO: 1 - TEMPO UTILIZADO: 00:26:32 | ||
Um sistema é representado pelo diagrama de blocos abaixo:
 Para determinar sua função de transferência, foram realizados os seguintes passos para redução do diagrama a um único bloco.  Analise os passos de redução do diagrama, e a seguir associe corretamente as colunas abaixo: |
|
| QUESTÃO: 1 - TEMPO UTILIZADO: 00:35:57 | ||
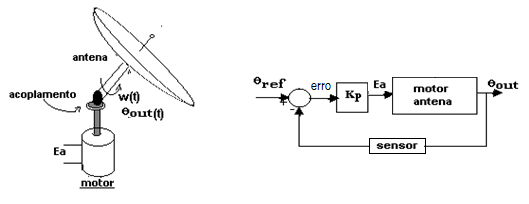
A figura abaixo mostra o diagrama de blocos de um servo-sistema posicionador de braço de robô.
 Tendo como referência a função de transferência C(s)/R(s), analise as afirmativas abaixo, marcando com V as verdadeiras, e F as falsas. |
||

|
F | O numerador da função de transferência é dado pelo polinômio (s+1). |

|
V | Os pólos do sistema são -0.5 + j0.87 e -0.5 - j0.87. |

|
F | O sistema tem apenas um zero, de valor -1. |

|
F | O ganho do servo-sistema é 10. |

|
V | O servosistema tem função de transferência de 2ª ordem. |

|
V | A equação caracterísitica do servosistema é s2+s+1=0 |

|
F | Se for aplicado um degrau unitário na entrada, a posição final da saída do servosistema tenderá a 10. |
4ª AA
| QUESTÃO: 1 - TEMPO UTILIZADO: | ||
A figura abaixo apresenta três respostas típicas de sistemas de primeira ordem, a entradas do tipo degrau unitário, numeradas com 1, 2 e 3.
 Considerando c(t) a variável de saída e t a variável tempo, analise as afirmativas: I - As respostas 1 e 2 são de sistemas com a mesma constante de tempo, porém com ganhos diferentes, enquanto que as respostas 2 e 3 são de sistemas com o mesmo ganho, porém com constantes de tempos diferentes. II - As respostas 1 e 3 são de sistemas com constantes de tempo e ganhos diferentes, enquanto que as respostas 2 e 3 são de sistemas com a mesma constante de tempo, porém com ganhos diferentes III - As respostas 2 e 3 são de sistemas com constantes de tempo diferentes, porém com ganhos iguais, enquanto que as respostas 1 e 3 são de sistemas com constantes de tempo iguais e ganhos diferentes. Estão corretas as afirmativas: |
||
| II e III | ||
| I e III | ||
| I e II | ||

|
I apenas. | |
| II apenas. | ||

| QUESTÃO: 1 | ||
Encontre a transformada de Laplace da EDO abaixo.
2.dH(t)²/dt²+4.H(t)=g(t) onde: dH(0)/dt=0 H(0)=0 |
||
| H(s)/g(s)=1/(2.s+4) | ||
| H(s)/g(s)=1/(2.s²+2) | ||

|
H(s)/g(s)=1/(2.s²+4) | |
| H(s)/g(s)=2/(2.s²+4) | ||
| H(s)/g(s)=1/(4.s²+4) | ||
| QUESTÃO: 2 | ||
Encontre a transformada de Laplace da EDO abaixo.
dH(t)²/dt²+H(t)=2.g(t) onde: dH(0)/dt=0 H(0)=0 |
||
| H(s)/g(s)=2/(s²+2) | ||
| H(s)/g(s)=2/(s+1) | ||
| H(s)/g(s)=1/(s²+1) | ||

|
H(s)/g(s)=2/(s²+1) | |
| H(s)/g(s)=2/(s³+1) | ||
6ª ACQF
| QUESTÃO: 1 | ||
Encontre o diagrama de bloco equivalente para a estrutura abaixo, e assinale a alternativa correta:
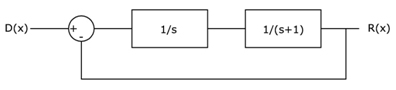 |
||
| R(s)/D(s)=2/(s²+s+2) | ||
| R(s)/D(s)=1/(s²+s) | ||
| R(s)/D(s)=2/(s²+s+1) | ||
| R(s)/D(s)=1/(s²+2.s+1) | ||

|
R(s)/D(s)=1/(s²+s+1) | |
|
| QUESTÃO: 1 - TEMPO UTILIZADO: 00:01:03 | ||
Considere o lugar das raízes de um sistema de controle com realimentação unitária, e controlador com ganho variável G dado na figura abaixo.
 Analisando o gráfico dado, é incorreto afirmar que: | ||
 | Para G<9, o sistema terá pólos reais e distintos. | |
 | O valor aproximado de G que coloca o sistema no limite da estabilidade é G=2.91. | |
| Para 2.91<G<9, o sistema é oscilatório, pois os pólos são complexos conjugados. | ||
| O valor de G que torna os pólos do sistema reais e iguais é G=9. | ||
| O sistema será instável para G<2.91. | ||
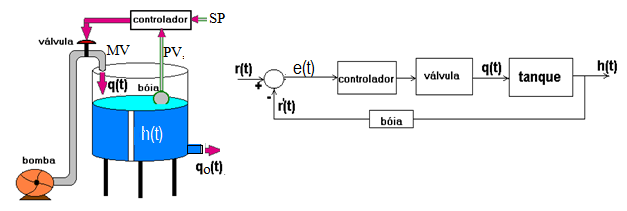
| QUESTÃO: 2 - TEMPO UTILIZADO: 00:00:26 | ||
O gráfico do lugar das raízes de um sistema de controle com realimentação unitária, e com controlador é do tipo proporcional, é dado na figura abaixo:
 Quanto aos pólos do sistema, dependendo do valor de K, é correto afirmar que: | ||
| Podem tender à região de instabilidade, se o valor de K for muito alto. | ||
 | Podem ser reais e distintos, reais e iguais, ou complexos conjugados. | |
 | Podem tornar-se puramente imaginários. | |
| Podem tender todos ao infinito, se o valor de K for muito alto. | ||
| Não há possibilidade de ter pólos dominantes no sistema. | ||
| QUESTÃO: 3 - TEMPO UTILIZADO: 00:00:20 | ||
Na figura é apresentado o gráfico do lugar das raízes de um sistema de controle, com realimentação unitária e controlador com parâmetro ajustável K.
 Considerando valores de K para sistema oscilatório, o aumento do ganho do controlador pode provocar vários efeitos na resposta do sistema. Marque a opção incorreta. | ||
| Melhorar a estabilidade do sistema. | ||
| Eliminar as oscilações. | ||
 | Aumentar a frequência das oscilações. | |
 | Reduzir o overshoot. | |
| Reduzir o tempo de resposta transitória. | ||
| QUESTÃO: 1 | ||
Um bloco denominado
"A "está em uma dada estrutura de blocos que resulta em um bloco
equivalente igual a Y(s)/R(s)=A/(1-A), qual o nome desta estrutura.
|
||
| Soma | ||
| Realimentação negativa | ||
| Divisão | ||

|
Realimentação positiva | |
| Subtração | ||
| QUESTÃO: 2 | ||
Encontre o bloco equivalente do diagrama abaixo, e marque a opção correta:
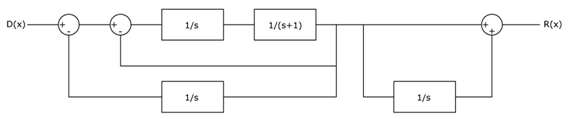 |
||
| R(s)/D(s)=1/(s(s(s+2)+1)+1) | ||
| R(s)/D(s)=2/(s(s(s+1)+1)+1) | ||

|
R(s)/D(s)=1/(s(s(s+1)+1)+1) | |
| R(s)/D(s)=s/(s(s(s+2)+1)+1) | ||
| R(s)/D(s)=s/(s(s(s+1)+1)+1) | ||
| QUESTÃO: 3 | ||
Um bloco denominado
"A "está em uma dada estrutura de blocos que resulta em um bloco
equivalente igual a Y(s)/R(s)=A/(1+A), qual o nome desta estrutura.
|
||
| Divisão | ||
| Somatória | ||
| Realimentação Positiva | ||

|
Realimentação Negativa | |
| Subtração | ||
QUESTÃO 01
Dada a G(s) abaixo, determine os
valores aproximadosdos parâmetros para um controlador PI usando o
coeficiente IAG. Assinale a alternativa correta.
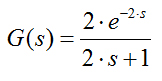
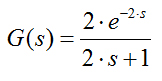
| Kc=0.291 e |
|
| Kc=0.492 e |
|
| Kc=0.1 e |
|
| Kc=0.492 e |
|
| Kc=0.492 e |
8ª ACQF
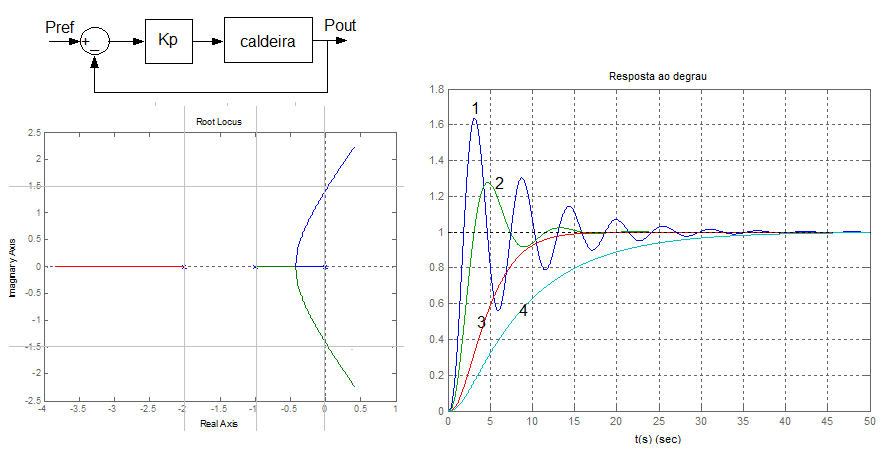
QUESTÃO 01
O conjunto de figuras a seguir apresenta informações sobre um sistema de controle de pressão em uma caldeira utilizada para geração de vapor. São dados o diagrama de blocos do sistema de controle, o gráfico do lugar das raízes em função da variação do parâmetro Kp, e ainda respostas ao degrau do sistema, para alguns valores de Kp.
I - O valor aproximado de K=5.9 separa os comportamentos monótono e oscilatório da resposta do sistema, enquanto que o valor aproximado de K=0.38 separa o comportamento de respostas estáveis e instáveis
II - As curvas de resposta 1 e 2 foram obtidas para valores de K entre 0.38 e 5.9, aproximadamente, pois, para esta faixa de valores, o sistema possui pólos conjugados, e portanto apresenta respostas oscilatórias
III - As curvas de resposta 3 e 4 foram obtidas para valores de K entre 0.e 0.38 aproximadamente, pois, para esta faixa de valores, o sistema possui pólos reais.
IV - O valor limite de K utilizado para gerar o gráfico do lugar das raízes dado é aproxidamente K=17
Estão corretas as afirmativas:
|
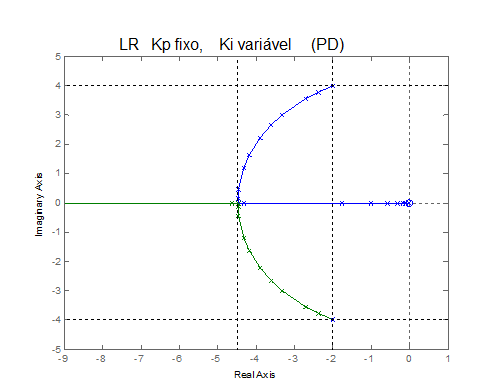
| QUESTÃO: 1 - TEMPO UTILIZADO: 00:00:53 | ||
Um determinado processo apresenta modelo de segunda ordem subamortecido, com pólos complexos conjugados dados por P1= -2 ± j * 2.45 e ganho= 0.1 .
Um controlador proporcional-derivativo, é inserido em uma malha de controle para controlar a saída deste processo, com realimentação unitária, de forma que a função de transferência de malha fechada torna-se:
FTMF(s)= (Kd.s+Kp)/(s2+4.s+10+Kd.s+Kp)
onde Kp é o ganho proporcional, e Kd o ganho derivativo do contrador PD.
Utilizando Kp= 10, foi construído o gráfico do lugar das raízes para o sistema, para variações do ganho Kd, o qual está apresentado abaixo:
Analise as informações e o gráfico do lugar das raízes dado, e dentre as alternativas a seguir, marque a incorreta.
| ||
| O aumento de Kd aumenta fator de amortecimento do sistema. | ||
| A ação derivativa contribui para reduzir overshoots na resposta do sistema. | ||
 | O aumento de Kd reduz o instante de ocorrência do máximo overshoot na resposta do sistema. | |
 |
Valores elevados de Kd contribuem para eliminar o erro de regime na resposta do sistema.
| |
| O aumento de Kd pode contribuir para a redução do tempo de acomodação do sistema. | ||
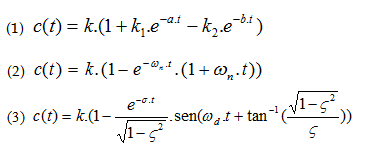
.png)


Um diagrama de blocos possui como função de transferência F(s) resultante, oriunda de uma realimentação negativa de valor 1, a alternativa que representa a função antes de ser reduzida é:
ResponderExcluirF(s) = 0.5/(10.s+1)
1/(20.s+1)
0.25/(10.s+1)
0.5/(20.s+1)
0.5/(10.s+1)
1/(10.s+1)
Como que resolver essa questão?
Por meio da função transferência, determine as constantes de controle proporcional e derivativo (PD). G(s)= kp/s³+2s²+3s+kp
ResponderExcluirKp = 1,6 e Ti = 0,45.
ResponderExcluirKp = 3,6 e Ti = 0,9.
Kp = 7,6 e Ti = 0,45.
Kp = 3,6 e Ti = 0,45.
Kp = 3,6 e Ti = 0,8.